Public Key Cryptography and PuTTYgen – Program for Generating Private and Public Keys

May 2, 2014 by

Jayanthi

In today's electronic world where everything is done online, "trust" is hard to come by. Conversations can be snooped on, credit card numbers can be stolen, identities can be exchanged and unseen eyes are everywhere. Imagine business emails being maliciously read by competitors, company's proposals being leaked and even crucial corporate information being tampered with...

This is where cryptography plays a crucial role, and important transactions have to be encrypted with strong algorithms to prevent leakage of information. We will discuss the basics of cryptography, public key cryptography, the RSA algorithm and the 'PuTTYgen' program (which is used to create and public and private keys) in this paper.

Learn Applied Cryptography

Build your applied cryptography and cryptanalysis skills with 13 courses covering hashing, PKI, SSL/TLS, full disk encryption and more.

Start Learning

It is a commonly known fact that the field of cryptography involves two major models – the symmetric cipher model and the asymmetric cipher or public key cipher model. The major difference between the two models is that the symmetric cipher model uses the same key to encrypt and decrypt messages, and the asymmetric cipher model uses different keys for encryption and decryption. Some popular symmetric algorithms are DES (Data Encryption Standard), AES (Advanced Encryption Standard) and Blowfish. Similarly popular asymmetric cipher algorithms are RSA (which stands for Ron Rivest, Adi Shamir, and Leonard Adleman, who designed the algorithm), ElGamal and DSS (Digital Signal Standard).

Public Key Cryptography

The key concepts in public key cryptography are plain text, encryption algorithm, cipher text, decryption algorithm and the recovered text. In addition, we make use of the most important component of public key cryptography to encrypt and decrypt the text – the public and private keys. If one key is used to encrypt the text, the other key is used to decrypt the text. The public and private keys are mathematically connected. The public keys are normally managed by a trustworthy third party person. Some of the required features of public key cryptography are listed below:

1. The private key should be infeasible to be generated through the public key.
2. Both the private and public keys should be easy to generate.
3. Person 'X' (also popularly known as 'Bob') should easily be able to encrypt a message and send it to person 'Y' (also popularly known as 'Alice') using person 'Y''s public key.
4. Similarly, person 'Y' should easily be able to decrypt the message using their private key.
5. A hacker should find it impossible to recover the original text in spite of knowing the ciphertext and the public key.

Public key cryptography solves two of the symmetric cipher model's drawbacks:

1. The key distribution problem, which in the symmetric model is to figure a way to distribute the keys when a lot of people are involved. This is solved in the asymmetric model by having "key-value" pair.
2. The authentication problem (verifying that the message indeed came from where it should have come from), which is solved in the asymmetric key model by making use of "digital signatures".

   We will next see the RSA algorithm, which uses public key cryptography and is the basis of the PuTTYgen program.

RSA Algorithm

As already stated, 'RSA'- stands for Ron Rivest, Adi Shamir and Leonard Adleman, who designed the algorithm. Most cryptographic algorithms involve tremendous amount of mathematics and the RSA algorithm is no exception. The mathematics behind the RSA algorithm are explained below in a lucid and easy to understand form. The basic idea behind the RSA algorithm is that it:

• "is a block cipher;
• it uses very large prime numbers for key generation; and
• the generated keys are mathematically linked." (Walsh College, 2010)

  There are three steps in the RSA algorithm:

1. generating the public and private keys
2. encrypting the message
3. decrypting the message.

We will see a brief gist of generating the public and private keys in this paper.

Generating the public and private keys:

1. For the RSA algorithm to be highly successful, two large prime numbers are chosen ('u' and 'v')
2. The product of the two numbers is calculated:

   (n=u * v)

3. Totient of the product is calculated as:

   Φ(n)= (u-1) (v-1) where 'Φ' is the Greek symbol 'phi'.

4. Next, we need to find values for 'P' and 'Q' after which the two large prime numbers can be abandoned.

   P * Q = 1(mod Φ(n))

   The only condition here is that both 'P' and 'Q' must be relatively prime to Φ(n). Two numbers are relatively prime, if they have no common factors apart from 1.

   For example,

   GCD (15,10) = 5

   GCD (18,10) =2

   GCD (21, 10) = 1

   Now, 21 and 10 are relatively prime to each other or co-prime to each other.

   Step (d) seems to be a bit more complicated than it actually looks. This can be simplified and re-written, assuming 'P' to be 7:

   7 * Q = K * Φ(n) + 1, where 'K' can be any number.

   Now 'P' and 'R' are the public keys and 'Q' and 'R' become the private keys. (Prime Number Hide-and-Seek: How the RSA Cipher Works)

Explaining the RSA algorithm with an example:

1. We take two small prime numbers, 5 and 11, for this example.
2. n=(5*11)=55
3. "Φ(55) = (5 - 1) * (11 - 1) = 4 * 10 = 40.
4. Now, we need to find numbers ('P' and 'Q') to fit the equation:
   

   P * Q = 1 (mod 40).
   

   Now, 'P' and 'Q' must be relatively prime to 40. (Prime Number Hide-and-Seek: How the RSA Cipher Works)
5. If 'P' is considered as 7, and the unfamiliar modular mathematics are removed and replaced with a highly understandable equation,

   7 * Q = K * 40 + 1,

   We next consider 'Q' to be 23 which is the next prime number close to 40. 'P' and 'Q' should also not be congruent to mod 40.

   The equation now becomes,

   7 * 23 = 161

   And 'K' now becomes '4'.

   So, the primary keys are 7 and 55 and private keys are 23 and 55.

   The RSA algorithm is tough to crack if the keys are long. RSA keys are typically between 1024 – 2048 bits long, and a key length of 1024 bits is mostly sufficient for most calculations.

Attacks against RSA:

There are four different types of attacks that are possible against the RSA algorithm.

1. Brute force: This is trying different types of combinations to crack the keys. It is very difficult to crack the algorithm when the keys are large.
2. Mathematical attacks: This is equivalent to factoring the two large primes, which again has not been successful.
3. Timing attacks: The timing attack depends on the running time of the decryption algorithm.
4. Chosen ciphertext attacks: This type of attack is aimed at the properties of the algorithm. (Stallings)

We will next move onto PuTTygen – a program for generating public and private keys.

PuTTY

"PuTTY is an SSH and telnet client, developed originally by Simon Tatham for the Windows platform. PuTTY is open source software that is available with source code and is developed and supported by a group of volunteers." (Download PuTTY) It is used to generate public and private keys.

The PuTTY program can be downloaded from this link:

http://www.chiark.greenend.org.uk/~sgtatham/putty/download.html.

The following screenshot shows the opening screen of the PuTTY program.

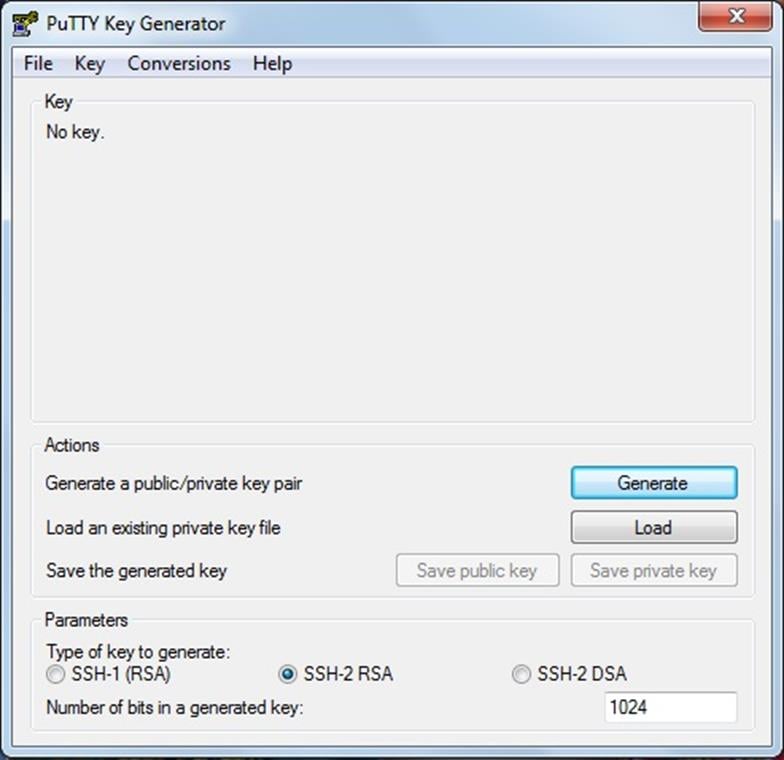
Before we move onto the other aspects of 'PuTTYgen' program, we will briefly divert to the topic of SSH. We can see from the above screenshot, that there are SSH-1 RSA and SSH-2 RSA and SSH2-2 DSA keys to generate. We will see a brief explanation of SSH next.

SSH

SSH is secure shell network protocol that is basically used to connect two networked computers securely. By means of SSH, the two computers can be used to perform remote and secure command login, secure data communication and other secure network services. SSH "connects, via a secure channel over an insecure network, a server and a client running SSH server and SSH client programs, respectively.^[1] The protocol specification distinguishes between two major versions that are referred to as SSH-1 and SSH-2." (Secure Shell)

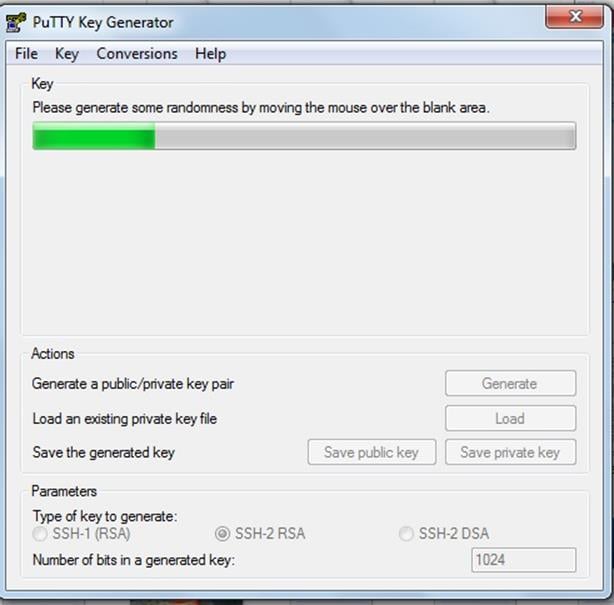
Retracing back to the PuTTY gen program, we can generate public and private keys by moving the mouse cursor constantly over the blank area.

The following screenshot shows the result of generating the public and private key pair:

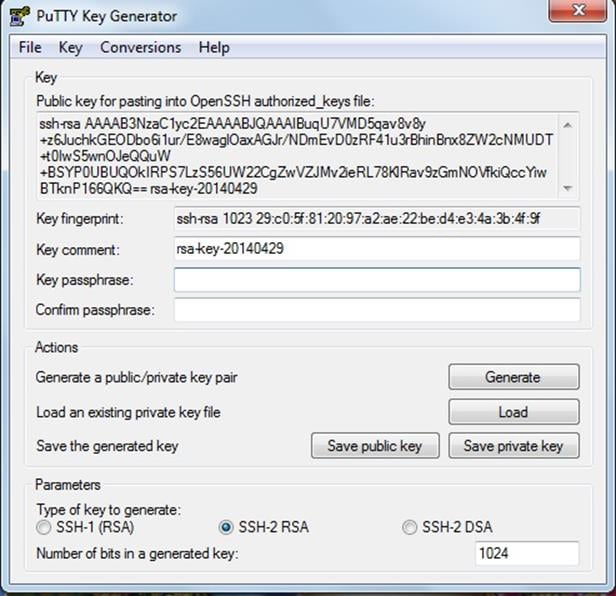
As we can see, we have generated SSH-2 RSA keys of length 1024 bits. The public and private keys can be saved as .txt files for later use. If the keys are generated using a length of 2048 bits, security will be enhanced, but at the cost of decreased performance.

The 'passphrase' field is optional, but it is better used. It is used to encrypt the private key in case it falls into wrong hands. The use of passphrase is explained in the University of Waterloo website which states that the private key is like a debit card and the passphrase is the PIN that is used to guard it.

"With SSH private keys, if somebody manages to acquire it, they will not be able to use it until they've figured out your passphrase. A private key without a passphrase is like a credit card, once they acquire it they can immediately use it." (SSH Public Key authentication)

Application of the keys generated:

The keys that are generated can be used for SSH authentication with OpenSSH. The public key is the one that will be stored on the server. The private key will be the key that will be stored on one's own computer. Instead of using the traditional username and password to login, the SSH client will authenticate your private key with the public key which was stored on the server.

Conclusion

This paper discussed the basics of cryptography and the necessities of cryptography, followed by the public key cryptography. We next moved onto the mathematics behind the RSA algorithm and concluded with the PuTTY program, which is used to generate public and private keys. Using public and private keys for authentication may be the future for online login into various websites.

Bibliography

Download PuTTY. (n.d.). Retrieved April 28, 2014, from putty.org: http://www.putty.org/

Prime Number Hide-and-Seek: How the RSA Cipher Works. (n.d.). Retrieved April 28, 2014, from muppetlabs.com: http://www.muppetlabs.com/~breadbox/txt/rsa.html#11

Secure Shell. (n.d.). Retrieved April 29, 2014, from en.wikipedia.org: http://en.wikipedia.org/wiki/Secure_Shell

SSH Public Key authentication. (n.d.). Retrieved from Waterloo Cheriton School of Computer Science: https://cs.uwaterloo.ca/cscf/howto/ssh/public_key/

Cryptography and Network Security. In W. Stallings.

Learn Applied Cryptography

Build your applied cryptography and cryptanalysis skills with 13 courses covering hashing, PKI, SSL/TLS, full disk encryption and more.

Start Learning

Walsh College. (2010). Retrieved from Walsh College.