Facebook Hacker Cup 2013 Qualification Round: Balanced Smileys
I must admit that I was a little bit hesitant whether or not I should enter the Facebook Hacker Cup, but I did it anyway just for the fun of it. There were three problems that needed to be solved and they were named "Beautiful Strings," "Balanced Smileys" and "Find the Min."
Presenting the Challenge

What should you learn next?
In this tutorial, I'll describe how I solved the Balanced Smileys challenge. The actual problem is described below:
[plain]
Your friend John uses a lot of emoticons when you talk to him on Messenger. In addition to being a person who likes to express himself through emoticons, he hates unbalanced parenthesis so much that it makes him go :(
Sometimes he puts emoticons within parentheses, and you find it hard to tell if a parenthesis really is a parenthesis or part of an emoticon.
A message has balanced parentheses if it consists of one of the following:
- An empty string ""
- One or more of the following characters: 'a' to 'z', ' ' (a space) or ':' (a colon)
- An open parenthesis '(', followed by a message with balanced parentheses, followed by a close parenthesis ')'
- A message with balanced parentheses followed by another message with balanced parentheses.
Write a program that determines if there is a way to interpret his message while leaving the parentheses balanced.
<strong>Input
</strong>
The first line of the input contains a number T (1 ≤ T ≤ 50), the number of test cases.
<strong>Output
</strong>
<strong>Constraints
</strong>
1 ≤ length of s ≤ 100
The example input is presented below:
[plain]
5
:((
i am sick today (:()
(:)
hacker cup: started :):)
)(
And its corresponding output is given below:
[plain]
Case #1: NO
Case #2: YES
Case #3: YES
Case #4: YES
Case #5: NO
Basically, we need to parse the messages from our friend John that are written in a file. The first line is the number representing the number of consecutive lines each containing a message from John. We need to decide whether the message contains balanced or unbalanced parentheses and write that as part of the output on stdout. The constant is that the message will not be longer than 100 characters, which is particularly important if we're writing the program in C/C++ where, if we're not careful, a buffer overflow condition can occur. We'll be writing the program in Python, so we don't actually need to worry about the mentioned constraint.
Solving the Problem
The most important thing of the challenge is the presented fact stating what constitutes a balanced parentheses and what it does not. The following facts need to be taken into account:
- An empty string ""
- One or more of the following characters: 'a' to 'z', ' ' (a space) or ':' (a colon)
- An open parenthesis '(', followed by a message with balanced parentheses, followed by a close parenthesis ')'
- A message with balanced parentheses followed by another message with balanced parentheses.
- A smiley face ":)" or a frowny face ":("
If you know about grammar, you can quickly write the corresponding code for the presented facts, which would simplify our life quite a bit, because we don't need to read the sentences all over again to check whether we've come up with the solution. All we need to do is take a look at the defined grammar. Using the grammars is the recommended way to do it if the program is correct, and that is what we'll be doing here.
The grammar can be very simple, like the one presented below:
[plain]
expr ::= lparen expr rparen | expr term | term
term ::= empty | string | smiley | frowny
string = '[a-zA-Z: ]+'
smiley = ':)'
frowny = ':('
empty = 'n'
lparen = '('
rparen= ')'
Basically, we're presenting the whole string with the exprsymbol, which accepts the parentheses, followed by the symbol term, followed by another parenthesis, or two term symbols or one term symbol. The term symbol represents the actual strings that we can encounter in a message being sent by John. What we need to do is write a program that takes the message s as input as well as the above grammar and tell us whether the message matches the grammar or doesn't. If it does, then the parentheses are balanced, otherwise they are not.
Here we need a basic understanding of lex and yacc. Basically, lex is a lexer and yacc is yet another compiler (from the man page). Here, we'll take a look at PLY, which is a similar tool and provides two separate modules: lex.py and yacc.py, which can both be found in the PLY package. The lex is used to break input into a collection of tokens specified by a collection of regular expression rules, and the yacc is used to recognize language syntax that has been specified in the form of a context-free grammar.
PLY uses variables that start with "t_" to denote the tokens. These variables can be either strings or functions. If the variable is a string, then it is interpreted as a regular expression and the match value is the value for the token. If the variable is a function, then it is called with the matched token, which modifies the token in any way and returns it. If we don't return anything from the function, then the match is ignored. We'll come to the actual code in a minute and everything will be clearer.
First of all, we can see that the actual problem lies in the fact that the string can also contain the ':' character. This is because in the following example, we don't know which is the right token we need:
[plain]
(:abcd)
(ab:cd)
(abcd:)
The second test string is ok, because there's only one possibility: if the alphabet letters are surrounding the character ':', then the ':' itself must be part of the string. But the problem occurs with the first and the third scenario, where we don't actually know whether the ':' is part of the string or part of the smiley/frowny. Therefore, we must include two test cases in our code, where one chooses the string option and the other chooses the smiley/frowny option. If either of the cases is solved, then the grammar matches the whole string and we can output 'YES'; if neither of the test cases is correct, then the grammar is wrong and we must output 'NO.'
Let's slowly go over the working example now. We start the program by defining the tokens and regular expressions for tokens that will be used to parse the input strings. We can see this on the code below:
[python]
# A list of token names.
tokens = (
'STRING',
'SMILEY',
'FROWNY',
'LPAREN',
'RPAREN',
# Simple tokens.
t_STRING = r'[a-zA-Z ]+'
t_SMILEY = r':)'
t_FROWNY = r':('
t_LPAREN = r'('
# Error handling rule
def t_error(t):
print "Illegal character '%s'" % t.value[0]
t.lexer.skip(1)
The code above is necessary for the ply.lex to do its magic. We defined the tokens and then the regular expressions in variables that start with string 't_', that are afterwards used by ply.lex (as we already discussed). At the end, we're defining the error function, which is called if the lex can't match certain characters or whenever an error occurs.
Then, we declare the tokenize function, which accepts the actual string as an argument and uses the ply.lex to parse the input string into token types and returns them. In our case, the token types are STRING, LPAREN, RPAREN SMILEY and FROWNY. Because of the above limitation (the ':') character, the SMILEY and FROWNY are not actually used, but are included nevertheless.
[python]
def tokenize(s):
# Build the lexer.
lexer = lex.lex()
aa = []
# Tokenize
while True:
tok = lexer.token()
if not tok: break
return aa
[/python]
The next function is called is_valid() and accepts the previously generated array of token types. The function uses some mathematics to get over the array and tries to figure out if parentheses are balanced or not. Let's first present the function:
[python]
def is_valid(aa):
a = 0
b = 0
count = 0
for i in aa:
if i == 'LPAREN':
l1 = len([e for e in aa[count+1:] if e == 'RPAREN'])
l2 = len([e for e in aa[count+1:] if e == 'SMILEY'])
l3 = len([e for e in aa[count+1:] if e == 'LPAREN'])
l4 = len([e for e in aa[count+1:] if e == 'FROWNY'])
if ((a >= 0) or (a < 0 and abs(a)<=b)) and l1+l2>=l3:
a += 1
else:
return False
elif i == 'RPAREN':
if (a==0 and b>0) or (a > 0) or (a<0 and abs(a)+1<=b):
a -= 1
else:
return False
elif i == 'SMILEY':
c += 1
elif i == 'FROWNY':
b += 1
if a==0 or (a<0 and abs(a)<=b) or (a>0 and abs(a)<=c):
return True
else:
[/python]
First, we're initializing the a, b and c variables to 0 and afterwards, we're using the a variable for counting the ')' and '(' occurrences. If we stumble upon the ')' character, we're decreasing the variable a by one, but if we see '(' we increase the variable by one. We use the variable b to count the frownys and the variable c to count smileys. The most important part is where we stumble upon the LPAREN '(', where we must check a couple of things. If a is greater or equal to 0, we're fine and must only check if the l1+l2 is greater or equal to l3. This is necessary because of a string like this:
[plain]
((((()()):)
If we're located on the first character, which doesn't count, the l variables are like this:
l1 = 3
l2 = 1
l3 = 5
l4 = 0
We can see that it's not really relevant if we complete the scanning of the string, because we already know it's not going to validate correctly. This is because there's more '(' characters than ')' (actual left parentheses plus smileys) so the parentheses can never be balanced.
Let's take a look at the example on the picture below:
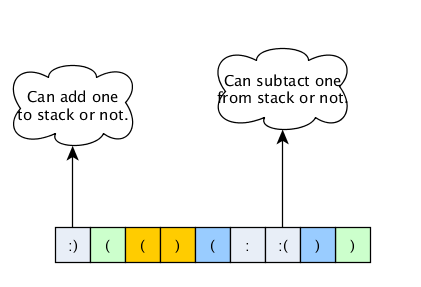
Here we can see that the :) character can add one or none parentheses to the stack, whereas the :( can also do the same, but with the other character. We can see that the above string has balanced parentheses. Let's take a look at another example, which closely resembles our code above:
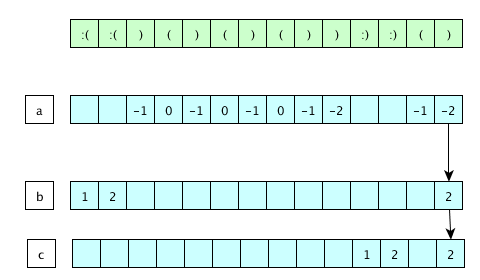
The first line is the actual string, whereas the next three lines constitute the variables a, b and c. The variable a is used to ++ and – to know where on the stack we're currently located. The variables b and c are only used for counting the smileys and frownys.
Let's present the whole program for the sake of completeness:
[python]
#!/usr/bin/python
import sys
import ply.lex as lex
# A list of token names.
tokens = (
'STRING',
'SMILEY',
'FROWNY',
'LPAREN',
'RPAREN',
'EMPTY',
# Simple tokens.
t_STRING = r'[a-zA-Z ]+'
t_SMILEY = r':)'
t_FROWNY = r':('
t_LPAREN = r'('
# Error handling rule
def t_error(t):
#print "Illegal character '%s'" % t.value[0]
def tokenize(s):
# Build the lexer.
lexer = lex.lex()
aa = []
# Tokenize
while True:
tok = lexer.token()
if not tok: break
return aa
def is_valid(aa):
a = 0
b = 0
count = 0
for i in aa:
if i == 'LPAREN':
l1 = len([e for e in aa[count+1:] if e == 'RPAREN'])
l2 = len([e for e in aa[count+1:] if e == 'SMILEY'])
l3 = len([e for e in aa[count+1:] if e == 'LPAREN'])
l4 = len([e for e in aa[count+1:] if e == 'FROWNY'])
if ((a >= 0) or (a < 0 and abs(a)<=b)) and l1+l2>=l3:
a += 1
else:
return False
elif i == 'RPAREN':
if (a==0 and b>0) or (a > 0) or (a<0 and abs(a)+1<=b):
a -= 1
else:
return False
elif i == 'SMILEY':
c += 1
elif i == 'FROWNY':
b += 1
if a==0 or (a<0 and abs(a)<=b) or (a>0 and abs(a)<=c):
return True
else:
count = 0
# foreach input string
for line in open(sys.argv[1]).readlines()[1:]:
count += 1
line = line.lower().replace('n', '')
# parametrize the line into smiley, frowny, lparen and rparen
aa = tokenize(line)
# go through the list
t = is_valid(aa)
if t:
print "Case #%d: YES" %(count)
else:
print "Case #%d: NO" %(count)
Conclusion
We can see that the challenge is not that hard; you just have to take the time to actually work through it. I intentionally used ply.lex because I wanted to know how it works, though I could have easily done the challenge without it (probably easier and more readable than it is now).
By the end of the day, we can say that it's like the time we were at the university, solving various problems for different assignments, which were very interesting and fun. This is just the same; it can't get any better than this. If you find this kind of stuff interesting, then I urge you to try to solve the problem by yourself or even optimize my solution.
References:
[1] Parsing with PLY, accessible at http://www.dalkescientific.com/writings/NBN/parsing_with_ply.html.
Become a Certified Ethical Hacker, guaranteed!
Get training from anywhere to earn your Certified Ethical Hacker (CEH) Certification — backed with an Exam Pass Guarantee.
[2] PLY, accessible at http://www.dabeaz.com/ply/ply.html.






